力扣17题-电话号码的字母组合-回溯算法题解

题目描述

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
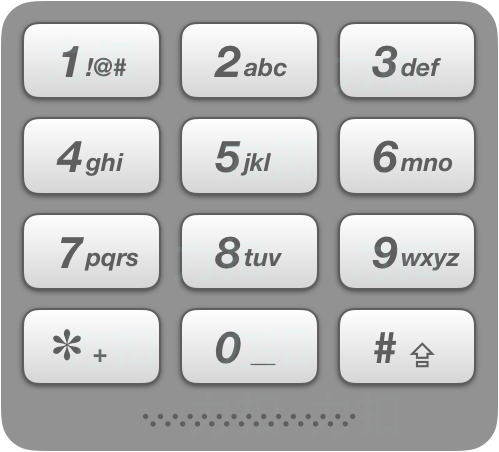
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

样例

1. 示例 1：
   输入：digits = "23"
   输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

2. 示例 2：
   输入：digits = ""
   输出：[]

3. 示例 3：
   输入：digits = "2"
   输出：["a","b","c"]

• 提示
  0 <= digits.length <= 4
  digits[i] 是范围 ['2', '9'] 的一个数字。

题目评估

知识点：DFS、递归、字符串、回溯算法
难度：中等

分析

本题实质是一个枚举组合的题目，只要是枚举组合就可以用回溯来递归一边求解，此时就可以用一个n叉树来表示枚举过程。（下图以样例1来做示范）

Java代码题解

//import java.util.ArrayList;
//import java.util.List;

class Solution {

    // 按键，注意索引和数字差2
    String[] mapper = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};

    List<String> res = null;  // 答案
    
    public List<String> letterCombinations(String digits) {
        res = new ArrayList<String>();
        
        if (digits == null || digits.length() == 0) {  // 空直接返回空
            return res;
        }

        char[] numbers = digits.toCharArray();  // 把字符串转换成字符数组
        char[] letters = digits.toCharArray();  // 这个数组用来放字母
        backtracking(numbers, letters, 0);      // 回溯

        return res;

    }

    public void backtracking(char[] numbers, char[] letters, int pointer){
        
        // pointer其实就是递归树的层数
        // 有几个数字递归树就有几层，如果pointer大于数字个数，就说明递归到叶子了
        if (pointer > numbers.length - 1) {
            res.add(new String(letters));
            return;
        }

        int num = (int)numbers[pointer] - 48;  // 把数字字符转换成整型数字

        for (int i = 0; i < mapper[num - 2].length(); i++) {  // 把按键num上的字母遍历一边
        	letters[pointer] = mapper[num - 2].charAt(i);  // 把遍历的字母装入letters数组中
            
            backtracking(numbers, letters, pointer + 1);  // 递归，此时pointer+1，处理下一层
        }

    }
}

力扣17题

复杂度分析

设m为3个字母的按键个数，n为4个字母的按键个数。
组合个数为3^m * 4^n，所以时间复杂度：O(3^m * 4^n)
递归需要占用栈空间，占用空间大小取决于递归树的层数，数字的个数就是递归树的层数，所以空间复杂度：O(n+m)