介绍
深度优先搜索(DFS,Depth-First Search)是搜索的手段之一。它从某个状态开始,不断地转移状态直到无法转移,然后回退到前一步的状态,继续转移到其他状态,如此不断重复,直至找到 最终的解。例如求解数独,首先在某个格子内填入适当的数字,然后再继续在下一个格子内填入 数字,如此继续下去。如果发现某个格子无解了,就放弃前一个格子上选择的数字,改用其他可 行的数字。根据深度优先搜索的特点,采用递归函数实现比较简单。
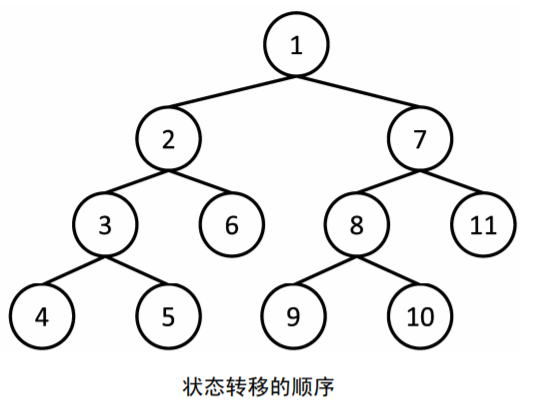
图示
示例题目1
部分和问题 给定整数 a1、a2、…、an,判断是否可以从中选出若干数,使它们的和恰好为 k。
限制条件
- 1 ≤ n ≤ 20
-10^8 ≤ ai ≤ 10^8
-10^8 ≤ k ≤ 10^8
样例1
输入
n=4
a={1,2,4,7}
k=13
输出
Yes (13 = 2 + 4 + 7)
样例2
输入
n=4
a={1,2,4,7}
k=15
输出
No
题解
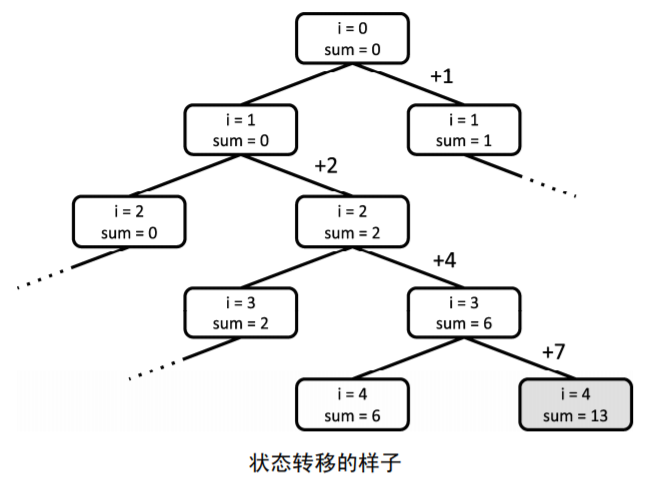
从a1开始按顺序决定每个数加或不加,在全部n个数都决定后再判断它们的和是不是k即可。因为状态数是2n+1,所以复杂度是O(2n)。如何实现这个搜索,请参见下面的代码。注意a的下标与题目描述中的下标偏移了1。在程序中使用的是0起始的下标规则,题目描述中则是1开始的,这一点要注意避免搞混。
题解代码
// 输入
int a[MAX_N];
int n, k;
// 已经从前i项得到了和sum,然后对于i项之后的进行分支
bool dfs(int i, int sum) {
// 如果前n项都计算过了,则返回sum是否与k相等
if (i == n) return sum == k;
// 不加上a[i]的情况
if (dfs(i + 1, sum)) return true;
// 加上a[i]的情况
if (dfs(i + 1, sum + a[i])) return true;
// 无论是否加上a[i]都不能凑成k就返回false
return false;
}
void solve() {
if (dfs(0, 0)) printf("Yes\n");
else printf("No\n");
}
示例题目2
Lake Counting (POJ No.2386) 有一个大小为 N×M 的园子,雨后积起了水。八连通的积水被认为是连接在一起> 的。请求出 园子里总共有多少水洼?(八连通指的是下图中相对 W 的*的部分)
* * *
*W*
* * *
限制条件
N, M ≤ 100
样例
输入
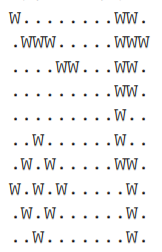
N=10, M=12 园子如下图('W'表示积水,'.'表示没有积水)
输出
3
题解
从任意的W开始,不停地把邻接的部分用'.'代替。1次DFS后与初始的这个W连接的所有W就都被替换成了'.',因此直到图中不再存在W为止,总共进行DFS的次数就是答案了。8个方向共对应了8种状态转移,每个格子作为DFS的参数至多被调用一次,所以复杂度为O(8×N×M)=O(N×M)。
题解代码
// 输入
int N, M;
char field[MAX_N][MAX_M + 1]; // 园子
// 现在位置(x,y)
void dfs(int x, int y) {
// 将现在所在位置替换为.
field[x][y] = '.';
// 循环遍历移动的8个方向
for (int dx = -1; dx <= 1; dx++) {
for (int dy = -1; dy <= 1; dy++) {
// 向x方向移动dx,向y方向移动dy,移动的结果为(nx,ny)
int nx = x + dx, ny = y + dy;
// 判断(nx,ny)是不是在园子内,以及是否有积水
if (0 <= nx && nx < N && 0 <= ny && ny < M && field[nx][ny] == 'W')
dfs(nx, ny);
}
}
return ;
}
void solve() {
int res = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (field[i][j] == 'W') {
// 从有W的地方开始dfs
dfs(i, j);
res++;
}
}
}
printf("%d\n", res);
}