题目描述
给定一个字符串s,找到其中最长的回文子序列,并返回该序列的长度。可以假设s的最大长度为1000 。
样例
-
示例 1:
输入:"bbbab"
输出:4
一个可能的最长回文子序列为 "bbbb"。 -
示例 2:
输入:"cbbd"
输出:2
一个可能的最长回文子序列为 "bb"。
题目评估
知识点:动态规划
难度:中等
分析
利用动态规划解题有以下四个步骤:
-
确定状态
我们可以开辟一个二维数组dp[i][j]表示从 i 到 j 子串的最长回文子序列的长度。 -
转移方程
我们可以发现,如果子串s[i..j]的两头字符s[i]和s[j]如果相等,那么s[i..j]的子串s[i+1..j-1]的最长回文子序列的长度+2后的值其实就是s[i..j]的最长回文子序列的长度,即dp[i][j] = dp[i+1][j-1] + 2。
但是,如果子串s[i..j]的两头字符s[i]和s[j]如果不相等,那么我们就取子串s[i+1..j]和s[i..j-1]两者中最长回文子序列长度最大的一个值赋给s[i..j]的最长回文子序列长度,即dp[i][j] = max( dp[i+1][j] , dp[i][j-1] )。 -
初始条件和边界情况
我们要知道,每个字符其实都是长度为1的回文子序列,所以dp[i][i]的值应该为1,然后i < j,但是在i > j的数组区域应该把所有值赋为0(java初始化就是0),因为当一个长度为2的串取子串dp[i+1][j-1]的时候i的值就会大于j,这时取到的值应该为0,而不是未定义。 -
计算顺序
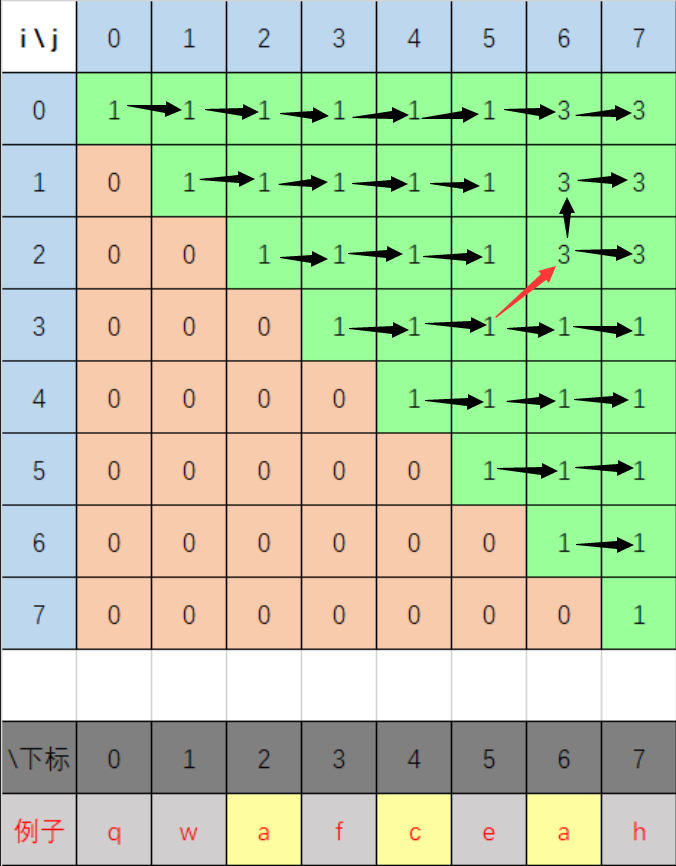
从整体来看,我们要从后往前计算,所有子串的头i应该从后往前移动,子串的尾应该从i + 1开始往后移动。
- 下图中黑色箭头代表复制值,红色箭头代表+2
Java代码题解
public class Main {
public static void main(String[] args) {
Solution s = new Solution();
int res = s.longestPalindromeSubseq("qwafceah");
System.out.println(res);
}
}
class Solution {
public int longestPalindromeSubseq(String s) {
// 定义一个字符串长度*字符串长度的二维数组,用来保存子串的最大回文子序列长度
int[][] dp = new int[s.length()][s.length()];
for (int i = dp.length - 1; i >= 0; i--) { // i从最后一个开始遍历
dp[i][i] = 1; // 初始化,每个字符都是长度为一的回文
for (int j = i + 1; j < dp[i].length; j++) { // j从第i+1个开始遍历
if (s.charAt(i) == s.charAt(j)) { // 如果子串的两头字符相等
// 该子串掐掉两头后的子串最大子回文序列长度+2就是该子串的最大回文子序列长度
dp[i][j] = dp[i + 1][j - 1] + 2;
} else { // 如果该子串两头字符不相等
// 该子串的两个掐掉一头的子串最大回文子序列长度,哪个最大,就取哪个赋给该子串最大回文子序列长度
dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
}
}
}
// 最后返回整个字符串的最大回文子序列长度
return dp[0][dp[0].length - 1];
}
}
复杂度分析
设n表示字符串长度,双层遍历一个二维数组,时间复杂度为O(n^2)
开辟了一个n*n的二维数组,空间复杂度为O(n^2)