发表于 | 分类于 | 0 | 阅读次数 22

分治简介

分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。即一种分目标完成程序算法，简单问题可用二分法完成。
归并排序就是分治的一种应用。

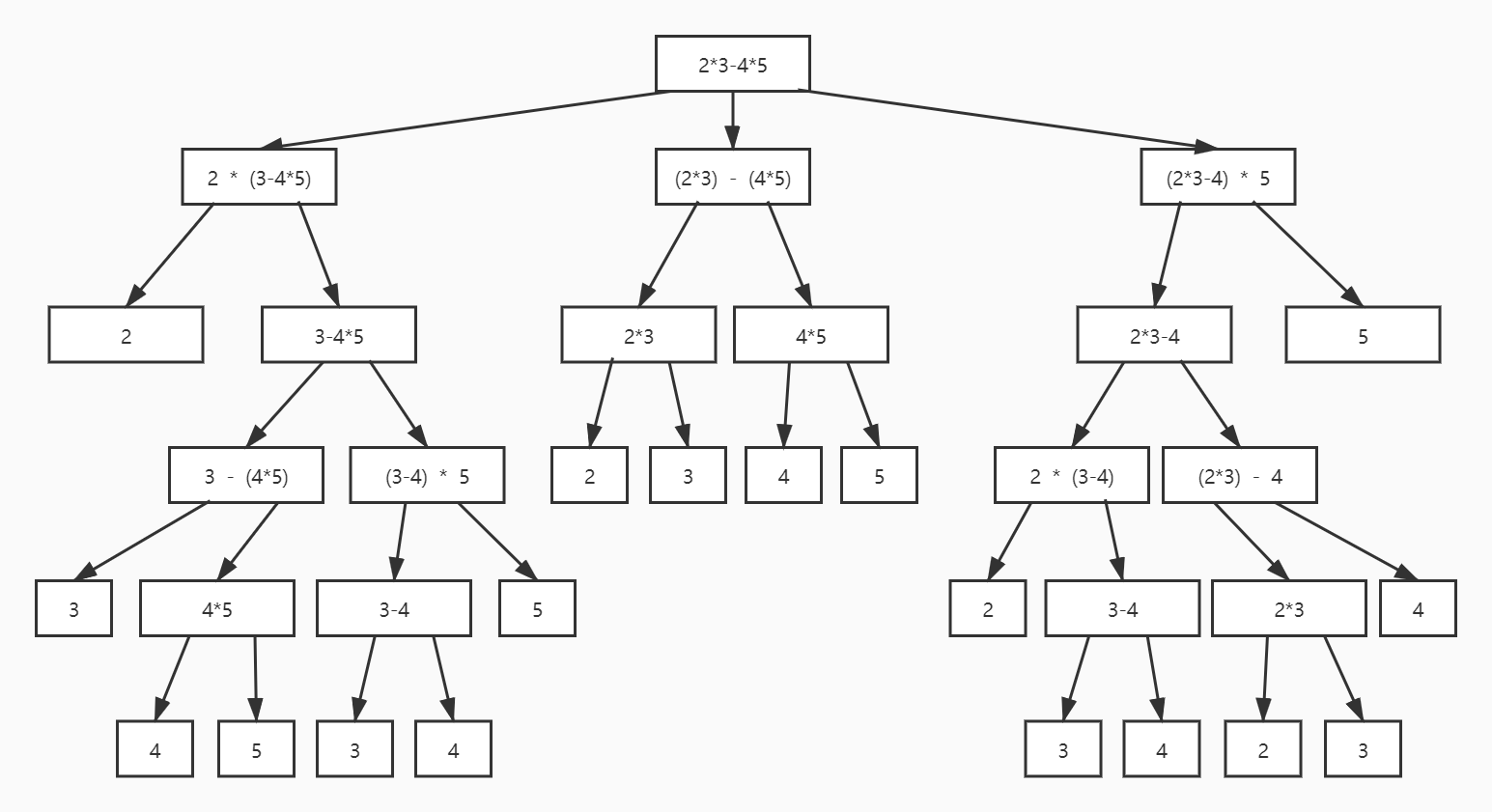
image.png

例题分析

例题

题目：为运算表达式设计优先级（题目来自力扣241题）
题干：给定一个含有数字和运算符的字符串，为表达式添加括号，改变其运算优先级以求出不同的结果。你需要给出所有可能的组合的结果。有效的运算符号包含+,-以及*。

样例1：
输入: "2-1-1"
输出: [0, 2]
解释:
((2-1)-1) = 0
(2-(1-1)) = 2

样例2：
输入: "23-45"
输出: [-34, -14, -10, -10, 10]
解释:
(2*(3-(45))) = -34
((23)-(45)) = -14
((2(3-4))5) = -10
(2((3-4)5)) = -10
(((23)-4)*5) = 10

题解

import java.util.List;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Map;

public class Question241 {
	public static void main(String[] args) {
		Solution241 s = new Solution241();
		List<Integer> res = s.diffWaysToCompute("2*3-4*5");
		System.out.println(res);
	}
}


class Solution241 {
	
	// 定义一个map用来记录每次计算的结果，存储为key:String, value:List的结构
    Map<String, List<Integer>> mem = new HashMap<String, List<Integer>>();
    
    public List<Integer> diffWaysToCompute(String expression) {
        
        if (mem.containsKey(expression)) {  // 每次调用方法时，先查一下map有无记录
            return mem.get(expression);  // 如果有记录值直接返回
        }
        List<Integer> res = new ArrayList<Integer>();  // 定义一个List用来记录一个字符串的结果
        for (int i = 0; i < expression.length(); i++) {  // 遍历字符串的每个值
            char ch = expression.charAt(i);  // 去出这个字符
            if (ch == '+' || ch == '-' || ch == '*') {  // 如果是运算符
                List<Integer> leftres = diffWaysToCompute(expression.substring(0, i));    // 该运算符左侧进行递归（分治的核心操作）
                List<Integer> rightres = diffWaysToCompute(expression.substring(i + 1));  // 该运算符右侧进行递归
                // 注意：返回的是两个List的结果，其中存储的是结果，类型是Integer
                
                for (int x : leftres) {  // 二重循环遍历左右两个结果，将他们的值通过运算符ch进行运算操作
                    for (int y : rightres) {
                        if (ch == '+') {
                            res.add(x + y);
                        } else if (ch == '-') {
                            res.add(x - y);
                        } else {
                            res.add(x * y);
                        }
                    }
                }
            }
        }
        if (res.size() == 0) {  // 如果该字符串只有一个数字，就将其加入res
            res.add(Integer.parseInt(expression));
        }
        mem.put(expression, res);  // 最后记录一下本次方法执行得到的res
        return res;
    }
}
题解参考自该视频讲解

递归树状结构图

image